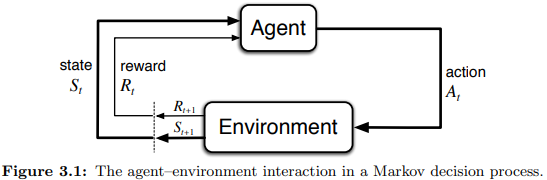
馬可夫決策過程
強化學習(Reinforcement Learning, RL)藉由互動學習如何行動以實現目標,而馬可夫決策過程(Markov decision processes, MDPs),是RL數學化的一種理想表示。MDPs中,代理(agent)與其環境(environment)在一連串分立的時步互動,其中代理是完全可知且可控的,而環境是不完全可控且很有可能難以理解的。代理與環境之互動遵循以下定義:
- 代理選擇動作(action)
- 動作的選擇基於狀態(states)
- 選擇的驗證基於回饋(rewards)
策略(policy)定義代理在給定狀態$S_t$下如何選擇動作$A_t$,而代理的目標為最大化期望回饋$G_t$。
$$G_t = R_{t+1}+R_{t+2}+R_{t+3}+\dotsb+R_T$$ $T$為最終時步,該形式如果再$T$極大時令$G_t$發散至無窮,所以實務上會使用以下形式:
$$ G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\dotsb=\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}, \text{ in } 0 \le \gamma \le 1 $$
$\gamma$為衰減係數。上式以遞迴形式表達:
$$ \begin{align*} G_t &= R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\dotsb \\ &= R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+\dotsb) \\ &= R_{t+1}+\gamma G_{t+1} \end{align*} $$
範例: $$ \begin{align*} \mathcal{S} &= \set{ \text{high}, \text{low} } \\ \mathcal{R} &= \set{ -3, 0, r_{\text{wait}}, r_{\text{search}} } \\ \mathcal{A(\text{hight})} &= \set{ \text{search}, \text{wait} } \\ \mathcal{A(\text{low})} &= \set{ \text{search}, \text{wait}, \text{recharge} } \\ \end{align*} $$
MDPs以表表示:

以轉移機率圖表示:

策略與價值函數
大部分的強化學習演算法需要價值函數,其估計代理在給定的狀態(或狀態-操作對)在未來的期望回饋總和,與策略有關。
策略將狀態$S$映射為每個可能操作的機率,如果代理在時間$t$遵循策略$\pi$,則$\pi(a|s)$即為在狀態$S_t=s$下操作為$A_t=a$機率。
策略$\pi$的狀態-價值函數 :
$$ \begin{align*} v_{\pi}(s) &= \mathbb{E}_{\pi} [G_t|S_t=s] \\ &= \mathbb{E}_{\pi} [\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}|S_t=s] \\ &= \sum_a \pi(a|s) \sum_{s^\prime, r} p[s^\prime, r|s, a](r+\gamma v_\pi(s^\prime)), \text{~for all } s \in \mathcal{S} \end{align*} $$
策略$\pi$的動作-價值函數 :
$$ \begin{align*} q_{\pi}(s, a) &= \mathbb{E}_{\pi}[G_t|S_t=s, A_t=a] \\ &= \mathbb{E}_{\pi}[\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}|S_t=s, A_t=a] \\ &= \mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})] \\ &= \sum_{s^\prime, r} p[s^\prime, r|s, a](r+\gamma v_\pi(s^\prime)) \end{align*} $$
最佳化策略和最佳化價值函數
解RL任務即為找一可以在長久運行下取得大量回饋的策略。如$\pi \ge \pi^\prime$,則$v_\pi(s) \ge v_{\pi^\prime}(s),~ s \in \mathcal{S}$必成立。最佳策略用$\pi^*$表示,其對應狀態-價值函數與動作-價值函數為:
$$v_*(s)= \max_\pi v_\pi(s),~ s \in \mathcal{S}$$
$$ \begin{align*} q_*(s, a) &= \max_\pi q_\pi(s, a) \\ &= \mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})] \end{align*} $$
以貝爾曼方程表示:
$$ \begin{align*} v^* &= \max_{a \in \mathcal{A}(s)} q_{\pi_*}(s, a) \\ &= \max_a \mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})] \\ &= \max_a \sum_{s^\prime, r} p[s^\prime, r|s, a](r+\gamma v_*(s^\prime)) \\ \end{align*} $$
$$ \begin{align*} q_*(s, a) &= \mathbb{E}[R_{t+1} + \gamma \max_{a^\prime} q_*(S_{t+1}, a^\prime) ] \\ &= \sum_{s^\prime, r} p[s^\prime, r|s, a](r + \gamma \max_{a^\prime} q_*(s^\prime, a^\prime)) \end{align*} $$
動態規劃
動態規劃(Dynamic Programming, DP)系指在給定MDP下,計算最優策略的算法統稱。在理論上非常重要,大部分RL算法由此延伸。
Policy Evaluation
給定$\pi$,如何計算$v_\pi$?
$$ \begin{align*} v_{k+1} (s) &= \mathbb{E}_\pi [R_{t+1} + \gamma v_k (S_{t+1})] \\ &= \sum_a \pi(a|s) \sum_{s^\prime, r} p[s^\prime, r|s, a](r + \gamma v_k(s^\prime)) \end{align*} $$
$k \rarr \infin$時,$v_k$收斂為$v_\pi$。
Policy Improvement
$$ \begin{align*} \pi^\prime (s) &= \argmax_a q_\pi (s, a) \\ &= \argmax_a \mathbb{E} [R_{t+1} + \gamma v_\pi (S_{t+1})] \\ &= \argmax_a \sum_{r^\prime, r} p(s^\prime, r | s, a) [r + \gamma v_\pi (s^\prime)] \end{align*} $$
$\epsilon$-greedy:
$$ \pi(s) = \begin{cases} \argmax_a Q (s, a) &\text{with probability } 1 − ε \\ random &\text{otherwise} \end{cases} $$
Policy Iteration
$$ \pi_0 \xrightarrow{\mathbb{E}} v_{\pi_0} \xrightarrow{\mathbb{I}} \pi_1 \xrightarrow{\mathbb{E}} v_{\pi_1} \xrightarrow{\mathbb{I}} \dotsb \xrightarrow{\mathbb{E}} v_{*} \xrightarrow{\mathbb{I}} \pi_{*} $$
$\xrightarrow{\mathbb{E}}$為Policy Evaluation,$\xrightarrow{\mathbb{I}}$為Policy Improvement,持續迭代取得$v_{*}$和$\pi_{*}$,虛擬碼如下:

蒙地卡羅方法與時序差分學習
蒙地卡羅方法(Monte Carlo, MC):
$$ V(S_t) \larr V(S_t) + \alpha [G_t - V(S_t)] $$
時序差分學習(Temporal Dierence, TD):
$$ V(S_t) \larr V(S_t) + \alpha [R_{t+1} + \gamma V(S_{t+1}) - V(S_t)] $$
$\alpha \in (0, 1]$為lr rate,MC遍歷所有狀態才更新$V(S)$,而TD在時步之間進行一次更新。
TD比MD收斂更快,TD在時步間即可快速優化$V$,而MC則須等待結束才可修正估計。
TD prediction methods for the control problem
The policy being learned about is called the target policy, and the policy used to generate behavior is called the behavior policy.
on-policy (learning is from data “on” the target policy)
off-policy (learning is from data “off” the target policy)
On-policy: Sarsa
Sarsa $(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})$:
$$ Q_{S_t, A_t} \larr Q(S_t, A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)] $$
Off-policy: Q-learning
$$ Q(S_t, A_t) \larr Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)] $$
Maximization Bias and Double Learning(Double Q-learning)
$q(s, a) \ne \max_a Q(s, a)$,因$Q$是隨機初始化的,且不能保證更新所有狀態組合。
$$ Q_1(S_t, A_t) \larr Q_1(S_t, A_t) + \alpha[R_{t+1} + \gamma Q_2(S_{t+1}, \argmax_a Q_1(S_{t+1}, a))-Q_1(S_t, A_t)] $$
$Q_1$和$Q_2$在不同的時步中會調換(通常是$50\%$的機率),同時在$Q_1$與$Q_2$ over estimate 的機率相較只有一個Q更低。